研究概要 | Takashi Okada, PhD

複雑な生命現象において、要素間の関係性（ネットワーク）や揺らぎ（個体差、偶然性）が、応答・情報伝達・進化といったシステム全体の振る舞いにどんな法則性を生むのかに関心を持って研究しています。

化学反応ネットワークのネットワーク構造と制御応答

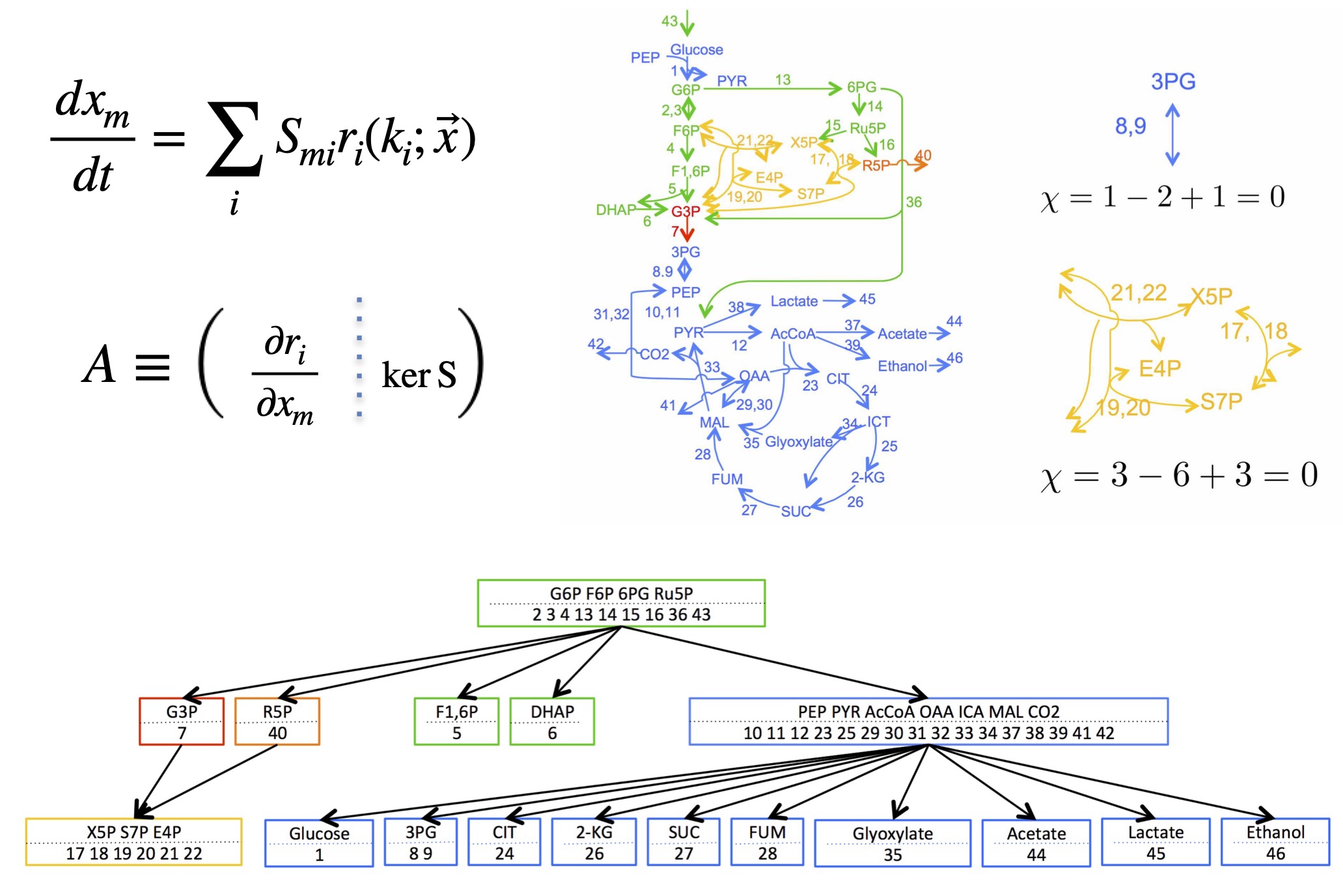
image-left

細胞の中では、化学反応どうしが「同じ物質（反応物や生成物）を共有する」ことでつながっていて、代謝経路のような大きなネットワークを作っています。

この研究では、酵素の働きを少し変えたときに、物質の濃度や反応の流れ（フラックス）がどれくらい変化するか（＝感度／応答）を、ネットワークのつながり方だけから予測できる理論を作りました。

その結果、変化が起きる場所（応答がゼロでない場所）の広がり方には、次の2つの特徴があることが分かりました。

局在化：定常状態に関して、酵素撹乱に対する影響はネットワーク全体に広がるわけではなく、オイラー数に類似した標数（分子の数ー反応の数＋サイクルの数＝０）をもつ特定の部分構造（緩衝構造）にとどまる。

階層性：緩衝構造が入れ子関係を形成することで、影響が「上流→下流」のように、段階的に伝わる

これらの結果は、生物が外からの変化に強い（頑健である）理由の一つが、ネットワークの構造そのものにあることを示唆しています。

また、緩衝構造は撹乱応答だけでなく、化学反応ネットワークにおける分岐現象（定常状態の多様性）を規定していることも分かりました。

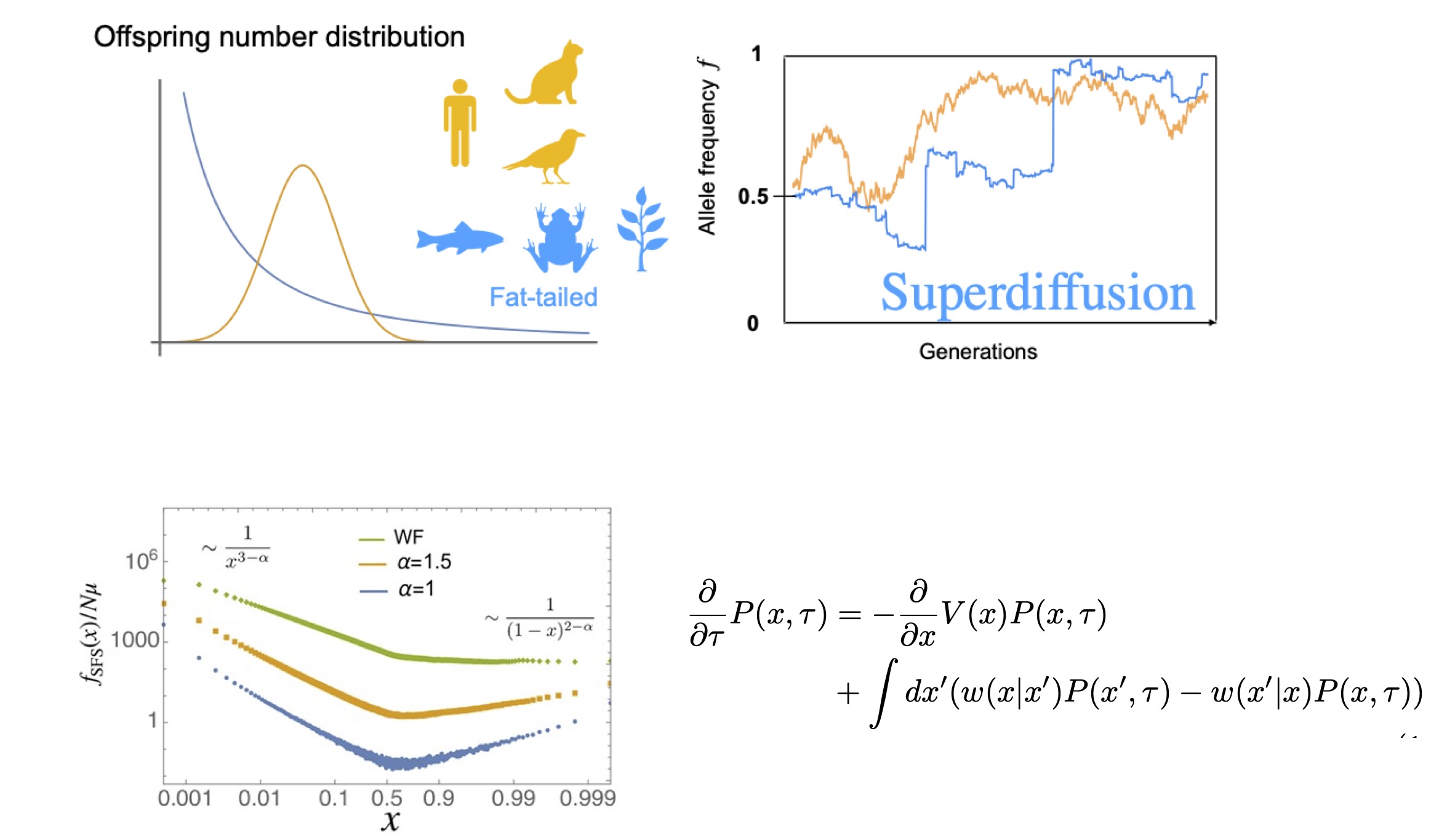
image-left

自然界の多くの集団では、子どもの数が個体ごとに大きく異なることが知られています。ほとんど子どもを残さない個体が多い一方で、ごく少数の個体が非常に多くの子どもを残す場合があります。こうした状況では、遺伝子の頻度が偶然によって大きく変動しやすくなります（これを遺伝的浮動と呼びます）。

しかし、これまでよく使われてきた集団遺伝学のモデルでは、「子どもの数のばらつきはそれほど大きくない」という仮定が置かれており、現実の集団で起きる大きな揺らぎを十分に説明できません。

過去をさかのぼる方向（どの個体が共通祖先か、など）については解析手法が発展していますが、時間を前に進めたとき（世代が進むとき）に、自然選択や突然変異と組み合わさって何が起きるのかについては、まだよく分かっていませんでした。

そこで本研究では、数学的な近似解析とスケーリングの考え方を用いて、子どもの数のばらつきが非常に大きい集団では、少数派の遺伝子が不利になりやすい「偏り」が自然に生じることを示しました。

この偏りは、各世代で「最も多く子どもを残した個体」がどれくらい多かったか、という点が時間とともに変化することから生まれます。その結果、自然選択や突然変異といった通常の要因と、この新しい偏りが競合し、遺伝子頻度が通常とは異なる仕方で揺らぐことが分かりました。

さらに、子どもの数がべき分布（ごく一部が極端に多くの子を残す分布）に従う場合について、遺伝子頻度の揺らぎの大きさ、遺伝子が集団に定着する確率、絶滅までの時間、観測される遺伝子頻度分布といった性質を、シンプルな数式関係（スケーリング則）として整理しました。

この研究は、「一部の個体が圧倒的に多く子孫を残す」集団で進化がどう進むのかを理解するための、新しい理論的な枠組みを与えるものです。

このような新しい進化の法則性は、微生物やウイルスのように世代交代が速い生物集団でも、実際に観測され始めています。これらの生物は、実験室内で進化の過程を直接調べる進化実験に利用できるため、理論と実験を結びつけて検証できる点でも非常に有望です。

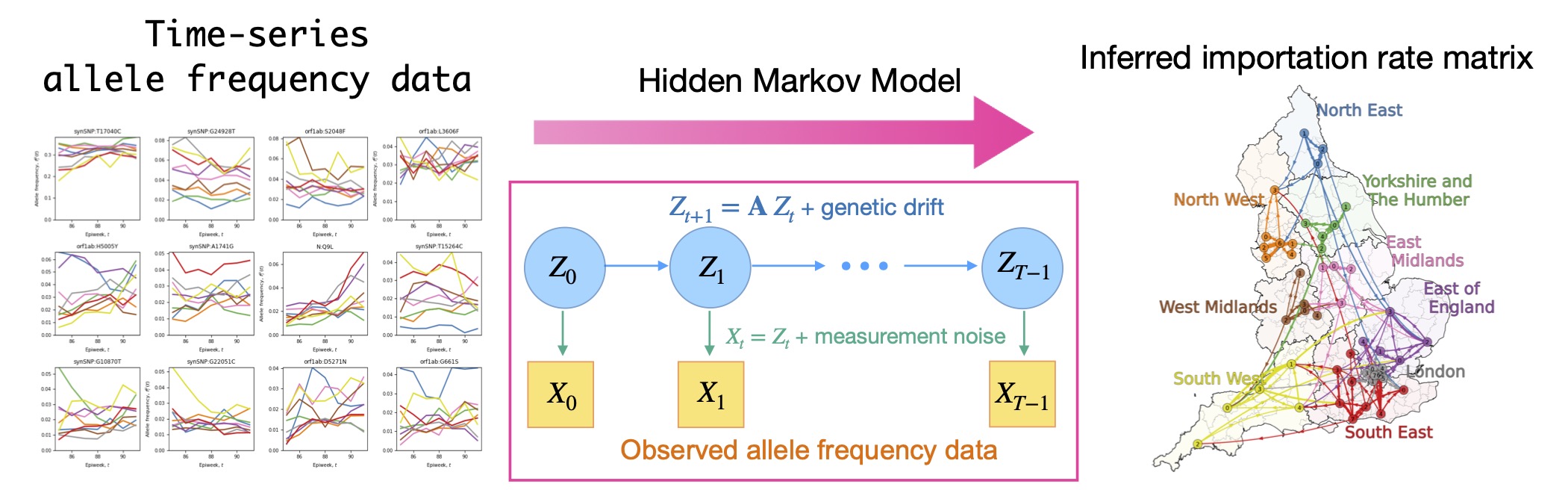
image-left

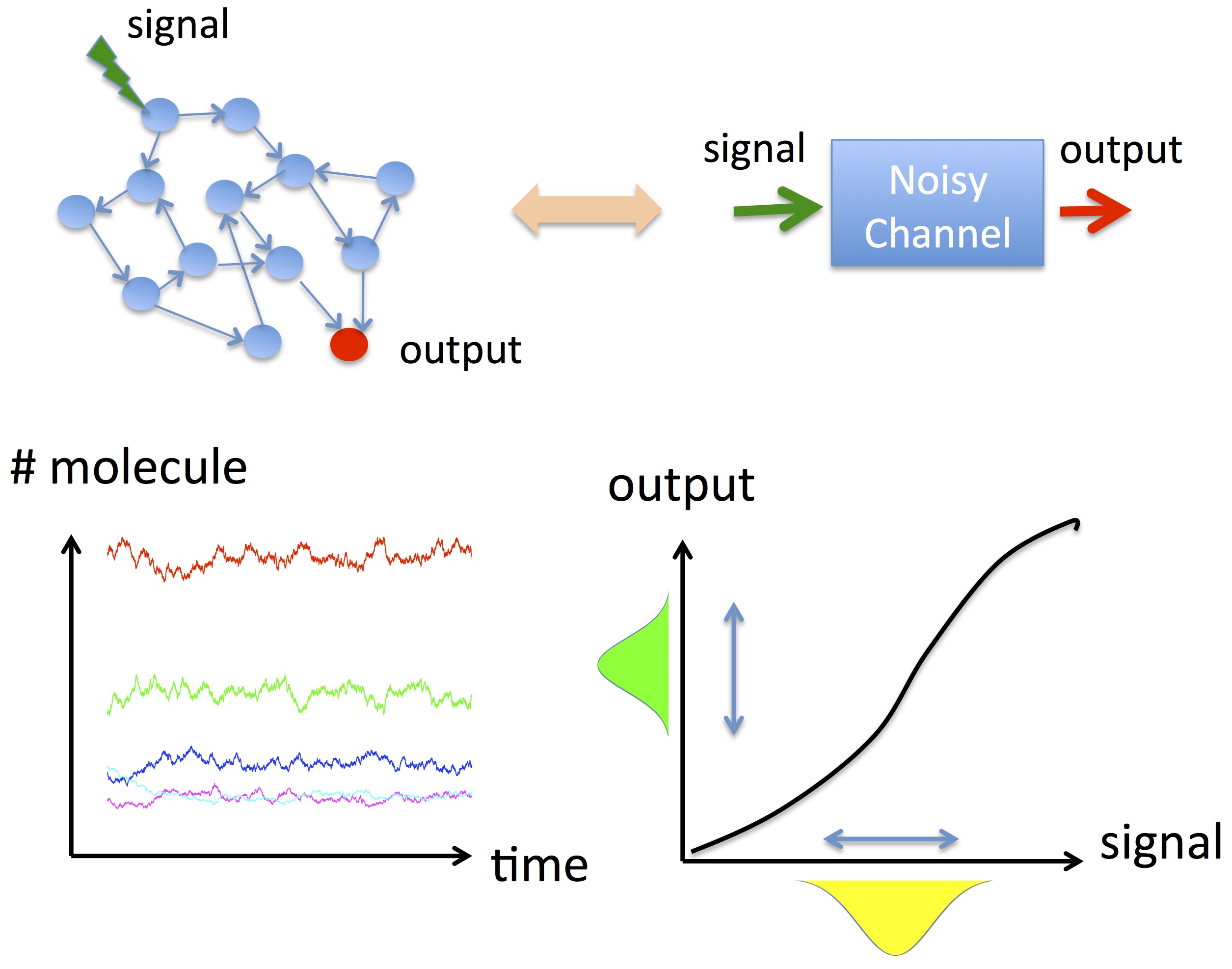
正確な情報伝達は、生物・社会・技術ネットワークに共通して重要な性質です。情報の流れを定量化する指標である転送エントロピー（Transfer Entropy）は、通常は小規模なネットワークであっても数値計算に頼る必要があり、なぜ情報がうまく伝わるのかという仕組みは分かりにくいままでした。

本研究では、確率的ブールネットワークを対象に、転送エントロピーを解析的に計算できる図式的な公式を導出しました。この手法は、信号から出力までの途中にあるネットワークが任意の構造を持ち、各ノードが異なる論理関数を持つ場合にも適用できます。

転送エントロピーをネットワークの構成要素ごとに分解して表すことで、情報がどの経路を通って伝わるのかという仕組みを明確化するとともに、情報伝達を最大化するネットワーク構造の設計原理を与えます。この結果は、生物ネットワークや人工システムなど、実在するネットワークの理解や設計に応用可能です。

現在は、この理論を実際の観測データや実ネットワークに適用し、実データに基づいた情報伝達の解析へと研究を発展させています。